O(n^2). По определению, это ограничение асимптотической сложности сверху, с точностью до константного множителя. То есть, это описание, на что примерно будет похоже поведение алгоритма на большом объеме данных. В случае пузырьковой сортировки – это значит, что чем больше размер n массива данных, тем ближе количество операций для его сортировки будет подходить (не превышая) к
(n*C)^2. Здесь C – любая фиксированная величина, не зависящая от n.Два важных вывода, которые следуют из этого определения:
1. Константный множитель из О-нотации можно (и принято) выбрасывать:
O(42*n) = O(n).2. "Недоминантный компонент" тоже можно выбросить:
O(n^2 + n) = O(n^2). Потому что n^2 + n < 2*n^2 при больших n.На практике "О большое" воспринимается как что-то вроде категории затратности. Например, два разных алгоритма поиска со сложностью
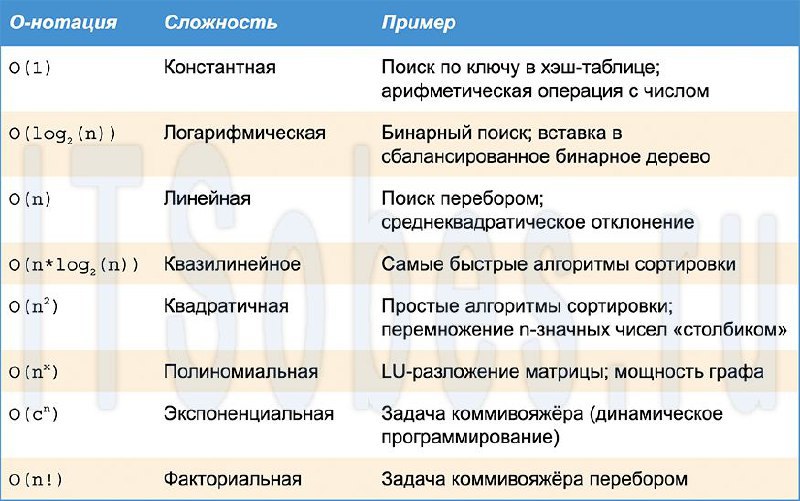
O(n) отработают за примерно одно время. Хранилище данных занимающее O(n!) потратит гигантский объем оперативной памяти по сравнению с альтернативой с O(log(n)).Вопросу понятия и применения асимптотической оценки сложности посвящена глава VI книги Cracking the Coding Interview. Вот некоторые примеры сложностей алгоритмов: